The name quadratic from the quadratic equation originates from “quad”. It means to square. Thus, in quadratic equations, you have to square the variables. Quadratic equations are polynomial equations. And it always includes an x². Consequently, it is known as the equation of degree because of the power 2 on the x.
This article will give you a rundown of the 3 easiest methods you can use to solve quadratic equations. So, let’s get started!
Standard Form of a Quadratic Equation
The standard form of the quadratic formula is as followed
ax²+bx+c=0
In the equation, a and b have known numeral values. Consequently, the value of a can never be 0. And x in the equation is the unknown variable whose value has to be found out.
Some examples of quadratic equations are given below
3x² + 6x + 3 = 0
In this equation, a=3, b=6 and c=3
x² – 5x = 0
This equation might look a bit tricky. However, it is much easier to solve. But you must be wondering where the value of a is?
Here, a=1 in the equation. And it is not shown, since we don’t usually write 1×2. Consequently, the value of c=0 while the value of b= -5.
Next,
6x-3=0
This formula is not a quadratic equation. But can you guess why? Because x2 is missing. And we know the fundamental of an equation being quadratic is that it must have an x² in the formula. Here, a=0. Thus, it is not a quadratic equation.
How to Solve Quadratic Equations?
The highest exponent of the variable in the quadratic equation has to be 2. And a quadratic equation can have two distinct real solutions. Moreover, it can also have two imaginary solutions or one double real solution.

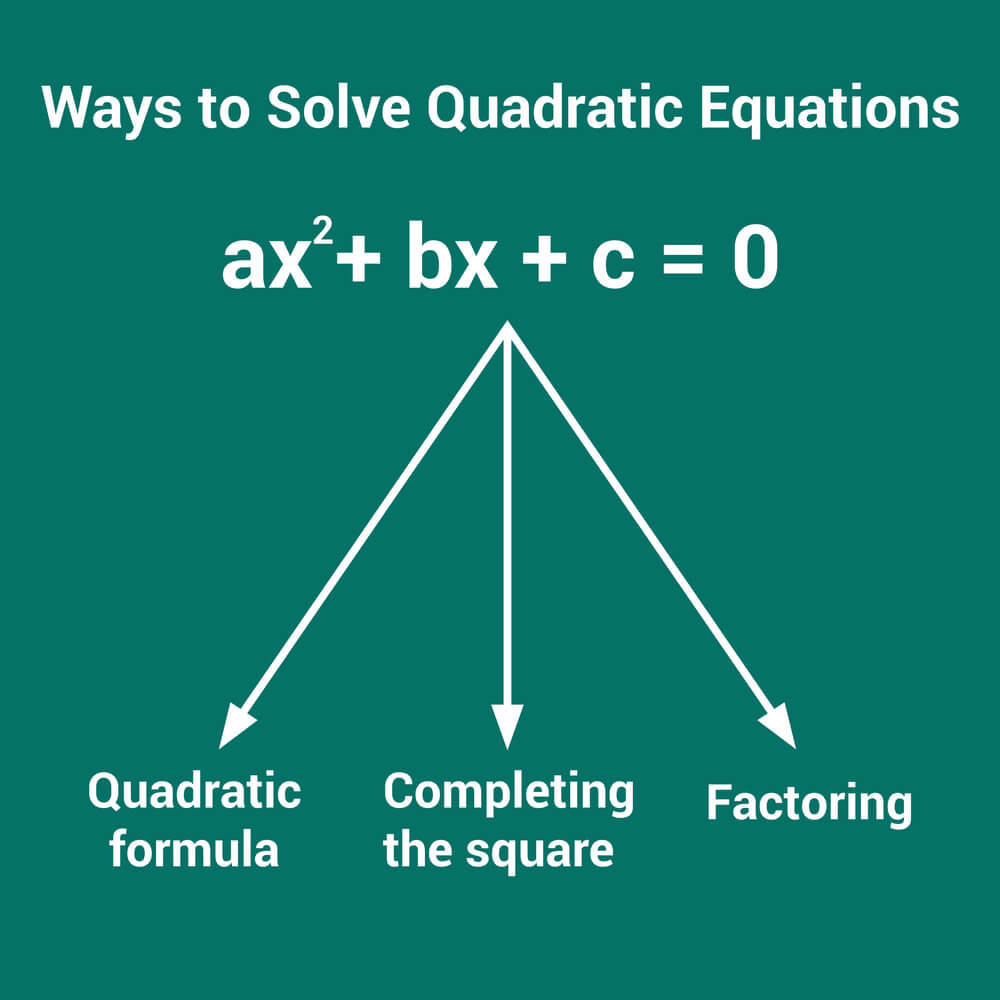
You can take the help of three main methods to solve a quadratic equation. These are,
1. Use the quadratic equation formula to solve
2. Factorisation of the quadratic equation if it is possible
3. Completion of the square.
You can master the three methods following a few simple steps.
Method 1: Use the Quadratic Equation Formula to Solve
4x²-5x-13=x²-5
4x²-x²-5x-13+5=0
3x²-5x-8=0
Move All the Terms to One Side of the Equation After Combining Them
The x² term has to be kept positive, while moving all the terms and values to one side of the equal sign. But the x² term has to come first. So, it is best if you write the equation in descending order of degrees. That way, x² will come first. Consequently, it should be followed by the term x and constant c.
Write the Quadratic Equation Formula
Factoring is not helpful for many quadratic equations. That is especially true when the roots of the equation are not rational numbers. So, the second step in solving quadratic equations requires you to use the quadratic formula.
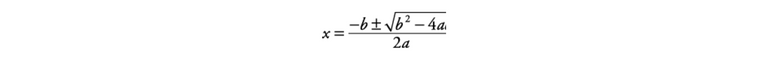
This is the quadratic equation formula.
Find Out the Value of the Variables a, b and c in the Equation
The coefficient of the x² is variable a. Consequently, the coefficient of the x term is b, and we have variable c as constant.
Thus, for the equation 3x² – 5x = 8 we have, 3x² – 5x -8 =0.
a=3
b= -5
c= -8
We have to set all terms with equal to 0.
Extract the Values of Variables a, b and c from the Equation
So, you now know the value of the three variables a, b and c. Now, you just have to plug in the values of the variables into the equation.
{-b+/- √ (b²- 4ac)} /2a
{- (-5) +/- √ ((-5)²- 4(3) (-8))} /2(3)
{- (-5) +/- √ ((-5)² – (96))} /2(3)
Solve the Problem
In the next step, you have to simplify the negative or positive signs by doing the remaining maths. Multiply or square the remaining terms after you have plugged in all the values. Go through the following steps.
- {- (-5) +/- √ ((-5)² – (96))} /2(3)
- {5 +/- √ (25 + 96)} /6
- {5 +/- √ (121)} /6
Simplification of the Square Root
You will be getting a whole number if the value under the root symbol is a perfect square. Consequently, simplify to the simplest radical form if the numeral is not a perfect square root. Moreover, the roots will be very complex if the number is of negative value.
For instance, in the example above, √ (121) = 11. Consequently, you can write,
x= (5 +/- 11) /6
Here, you get two different real numbers as roots. And it is due to the discriminant b² – 4ac being positive. Thus, the equation 3x² – 5x -8= 0 gives us irrational roots. Consequently, the quadratic equation formula can be used to produce rational roots. And it can be used for formulas that can give irrational roots.
Get the Solution for Positive and Negative Answers
After you have solved the problem of the square root symbol, you have to keep going. Continue solving the maths until you have found a positive and negative value for square roots. For example, you have a positive and negative option for x= (5 +/- 11) /6.
- (5+11) /6 = 16/6
- (5-11) /6 = -6/6
Simplify the Result
Divide the numbers by the largest number to get the simplified answer. Consequently, the largest number has to be evenly divisible into both numbers. Next, you can solve for x if you divide the first fraction by 2 and the second fraction by 6.
16/6 = 8/3
-6/6 = -1
x = -1, 8/3
To learn more about quadratic equations, take our High School Math Training course. The course curriculum introduces you to other fundamental topics of mathematics. The topic includes differentiation, linear equation and binomial theorem, among others. Consequently, the CPD accredited course provides you with exclusive tutor support. So, enrol today and start learning!
Method 2: Factorisation of Quadratic Equation
2x² – 8x – 4 = 3x – x²
2x² + x² – 8x – 3x – 4 = 0
3x² – 11x – 4 = 0
Move All the Terms to One Side of the Equation
Moving all the terms and values to one side of the equation is the first step to factoring an equation. However, you have to make sure the term x² remains positive. Now, move all the terms to one side by adding or subtracting the x² term, x term and constant. You have to make sure that nothing remains on the right side except 0.
Factor the problem
Now, you have to use the factor of the x² term and the constant term in order to factor the whole expression. Multiply the numeral values of the x² term and the constant term so that it equals the numeral value of middle term x.
- 3x² has one set of factors that is 3x and x.
- Plug in the factors of 4 using the elimination method. And it will help find a combination of -11x when multiplied. Since the constant is negative -4, so you can use the combination of -2 and 2. Also, you can use the combination of -4 and 1.
- Try the combination of factor (x – 4) (3x+1) using the trial and error method. The resultant factor will be 3x² -12x +1x -4. And the final middle term value after the addition and subtraction operation will be -11x.
- The trial and error method let you check a factor of combination before finding the correct factored quadratic equation.
Write Each Set of Parenthesis as Separate Equations
The two separate equations should equal 0. And it will generate two different values of x. (x-4) (3x + 1) = 0. Now, put the expression in each set of parentheses equal to 0 after factorising the equation. You have to do this to get 0 by multiplying. The principle rule or the property states that in the factored parenthesis, one factor must equal zero.
Thus, you should write it as 3x + 1= 0 and x- 4= 0.
Independent Solving of Each Zeroed Equation
There will always be two possible values for x for a quadratic equation. Isolate the variables to find the solution of x one by one. Now, write down the two solutions for x.
- Solve 3x+1= 0
3x = -1 …. Subtraction
3x/3 = -⅓ …. By division
X = -⅓ …… Simplification
- Solve x-4= 0
x = 4 …. Subtraction
So, the two solutions of x is -⅓ and 4.
Justify Both Parenthesis
The final step to solving your quadratic equation is to check and verify whether the solution for x is correct.
To check for whether x = -1/3 for quadratic equation (3x + 1) (x – 4) = 0:
(3[-1/3] + 1) ([-1/3] – 4) = 0 ….. substitution
(-1 + 1) (-4 1/3) = 0 ….. simplification
(0) (-4 1/3) = 0 ….. multiplication
therefore, 0 = 0
So, x= -⅓ is correct when both sides equal 0 in justification.
Next, check for whether x= 4 for quadratic equation (3x + 1) (x – 4) = 0:
(3[4] + 1) ([4] – 4) = 0 ….. by substitution process
(13) (4 – 4) = 0 ….. by simplification method
(13) (0) = 0 ….. by multiplication
Therefore, 0 = 0
The two different solutions check out correct when verified for variable x.
Watch this video to gather more ideas on how to solve quadratic equations by factoring.
Method 3: Completion of the Square
2x²- 9 = 12x
2x² – 12x – 9 = 0
Move All Terms to One Side of Equation
The x² term or a has to be positive. You can do so in the above-mentioned way. In the equation, 2 is the term for a, -12 is the term for b and -9 is the term for c.
Move the Constant to Another Side of the Equation
The numerical term without a variable is the constant term. Now, you have to shift the term to the right side of the equation.
2x² – 12x = 9
Coefficient of x² or a will Divide Both Sides of the Equation
If x² has no coefficient other than 1, no need to follow this step. But, in the case of this equation, the coefficient of x² is 2. So, you have to divide all the terms in the equation by 2.
2x² /2 – 12x/2 = 9/2
X² – 6x = 9/2
Divide, Square and Add the Result
You have to first divide the term b by 2. Consequently, the b term in this equation is -6. You can do it in the following way.
-6 /2 = -3
(-3)² = 9
X² -6x + 9 = 9/2 + 9
Simplification of Both Sides of the Equation
Factoring the term from the left side, you will get (x -3) (x- 3). Now you just have to add up the terms and get 9/2 + 9, or 9/2 + 18. The addition will result in 27/ 2 on the right side.
Square Root Both Sides
If you square root (x – 3)², the result will be (x- 3). Consequently, you can show the square root of 27/2 as +/- √ (27/2). So, the two square root values will be generated. Thus, x-3 = +/- √ (27/2),
Simplification of the Radical to Solve for X
The next step to solving the quadratic equation is to simplify the radical. So, you have to find a perfect square that is the factor of 27 and 2. Consequently, the square can be any number within 27 and 2. Finding the perfect square will help simplify the term,
+/- √ (27/ 2)
9 can be the perfect square as 9×3 =27. You can pull away the number 9 from the radical sign and write number 3 as the square root. 3 should be the fraction numerator placed under the root sign. Next, leave the 2 in the bottom and move the constant 3. And take the constant to the left of the equation. The final step for you will be to write down the two solutions you got for the x variable.
x= 3+ 3(√6)/ 2
x= 3- 3(√6)/ 2
Final Word
The central theme of algebra is a quadratic equation. You can use the three different methods of solving a quadratic equation, depending on the type of maths problem.
Consequently, remember that for a quadratic equation, you may find two different solutions or two different roots.